数学方法推导 leetcode 142 之环形链表 II

原题如下：

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改 链表。

我们知道，验证环形链表只需要快慢指针即可，但是在此基础上如何找到环的起始节点呢。

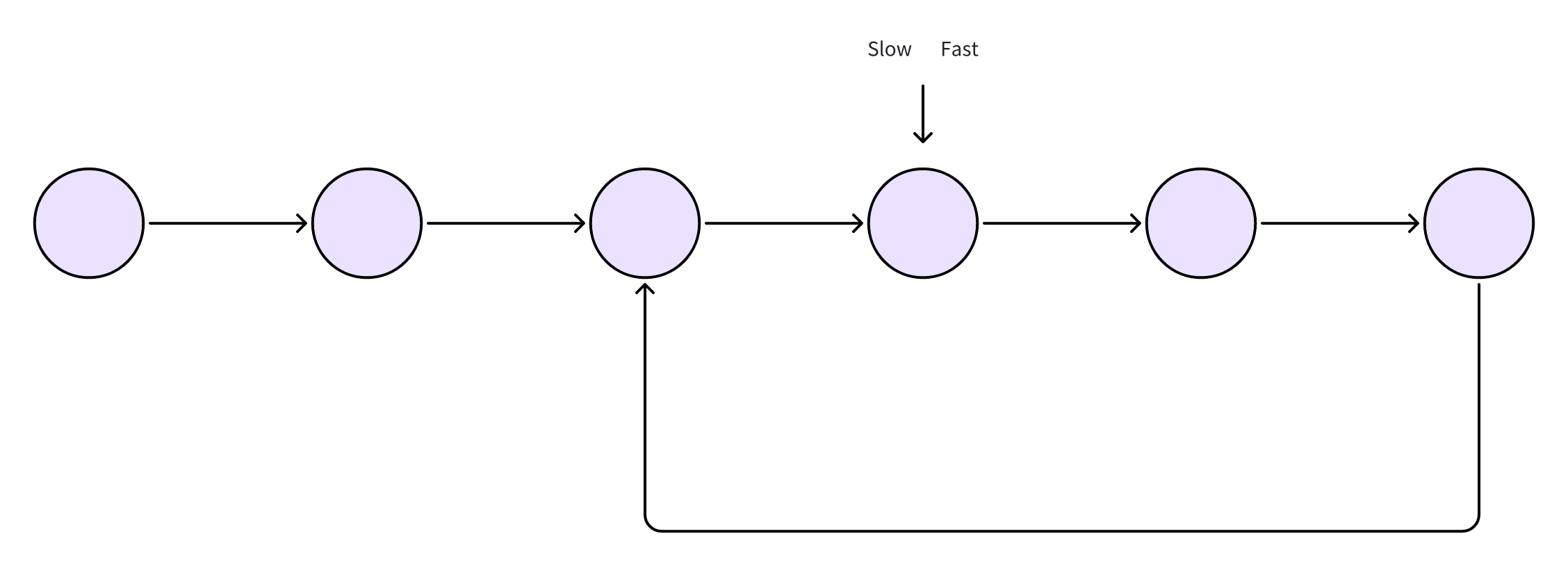
我们先假设环之前的节点数为 X，环中的节点数为 Y，既然快慢指针一定可以相会，那么在 K 步之后，慢指针的终点位置是

(K - X) % Y + X

快指针（初始位置在慢指针的下一个位置）的位置是

(1 + 2K - X) % Y+ X

既然二者相等，那么一定有（即慢指针比快指针少走的节点数一定是 Y 的整数倍）：

K - X + nY = 1 + 2K - X

也就是：

K = nY - 1

可见，快慢指针重合之前走过的步数，与 X 无关，只与 Y 无关，这也符合自觉。

我们要求什么呢，显然是环的起始位置 X。如果一个指针从链表的头节点开始走，一次走一个节点，只需要走 X 步 就可以抵达 X。

但现在我们不知道 X 的具体值。

我们实施看从两个指针的重合点开始，一次走一个节点，要走多少才能到达 X，假设步数为 P，那么有：

(nY - 1 - X + P) % Y + X = X

显然，P = X + 1 可以走到 X 节点，那么我们不妨这样，在两个指针重合之后，让快指针一次走一个节点，走 X+1 步，即可到达 X，但问题是我们仍然不知道 X 是多少。

没关系，我们可以把慢指针重置到链表的头部，然后让快指针先走一步，然后二者再同时走，相交节点即是 X，代码如下：

class ListNode {
    val: number
    next: ListNode | null
    constructor(val?: number, next?: ListNode | null) {
        this.val = (val===undefined ? 0 : val)
        this.next = (next===undefined ? null : next)
    }
}

function detectCycle(head: ListNode | null): ListNode | null {
    let slow = head;
    let fast = head?.next;
    while (slow && fast) {
        if (slow === fast) {
            slow = head;
            fast = fast.next; // 先向下走一步
            while (slow !== fast) { // 然后二者同时走，直到相会
                slow = slow.next;
                fast = fast.next;
            }
            return slow;
        }
        slow = slow.next;
        fast = fast.next?.next;
    }

    return null;
};